How to win a 2 player game of 'Are you a Robot'

Brute Forcing Card Games Using Monte Carlo Methods

TL;DR

This game is a prisoners dilemma with a twist, you should either zap your opponent 90% of the time or always shake. My CEO Nader brought us a game one day called Are You A Robot that was a game with the following rules.

We played a few games, and it started becoming easy for him to tell when I was the robot and when I was a human, and I started losing a bunch of times. It was apparent that I was super easy to read, so I had to come up with a strategy that could take this aspect out of the game. My initial strategy was to never look at my card and shake, to try to psyche my opponent into shaking my hand. While this strategy was initially effective, we calculated it inefficient since it helped win only ~30% of the time. If the opponent had the robot card, it was an instant win.

Intuitively, it seemed like there was an optimal strategy due to the simplicity of its rules. So while I was on a plane home for thanksgiving, I decided to code up a Monte Carlo Simulation of various simple game strategies and see how they fared against each other.

Although I'm sure there is a more precise way to solve this problem, I find that Monte Carlo simulations can expose game mechanics that are otherwise difficult to uncover. I can code up a simulation of this game and brute force the problem rather than use a precise tool to solve it perfectly.

The basic strategies that I wound up coming up with were:

• randomly choose between zap or shake
• always shake
• always zap (when possible, since robots can't zap)

I then played these strategies against each other 10,000 times and graphed how they performed against each other.

Always Shake never wins unless playing against Always Shake leads to the best outcome, the only one where both players win more than lose

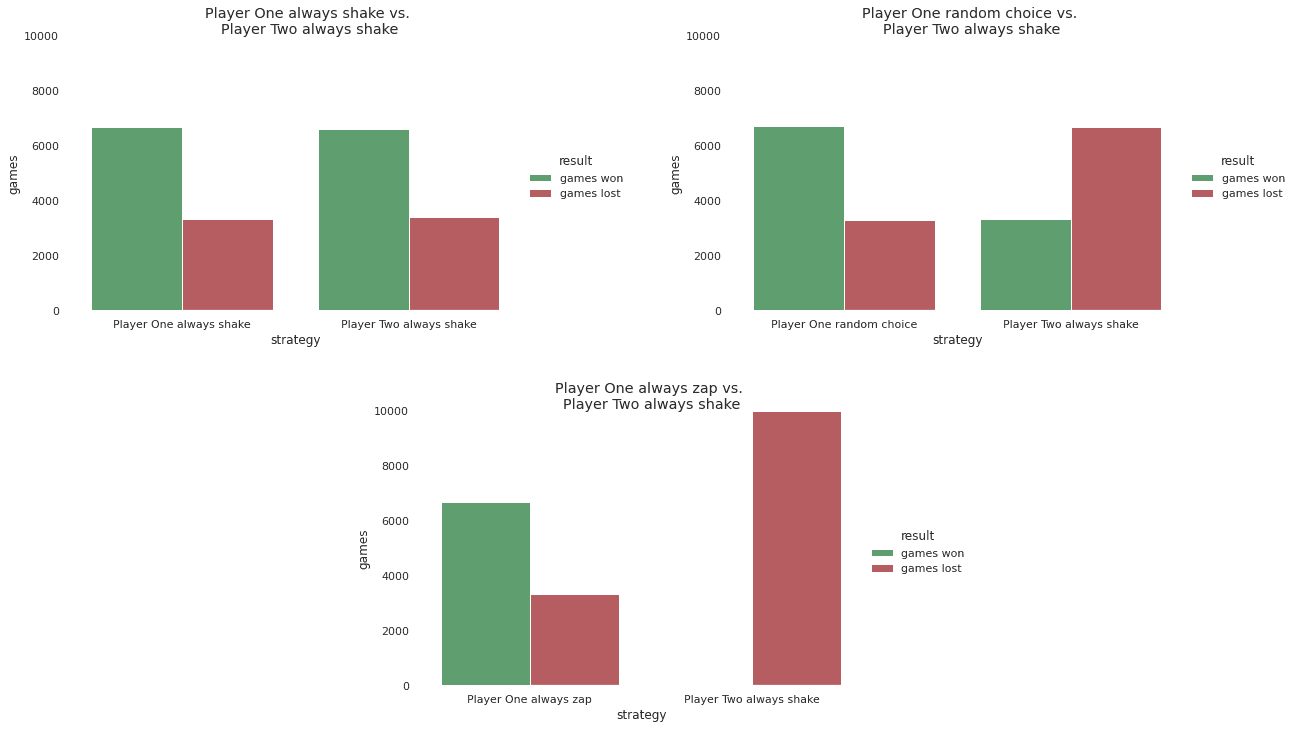
Always Zap wins the most and loses the least against each of the other strategies and reaches equilibrium when played against itself, but a lesser outcome when compared to both players playing Always Shake

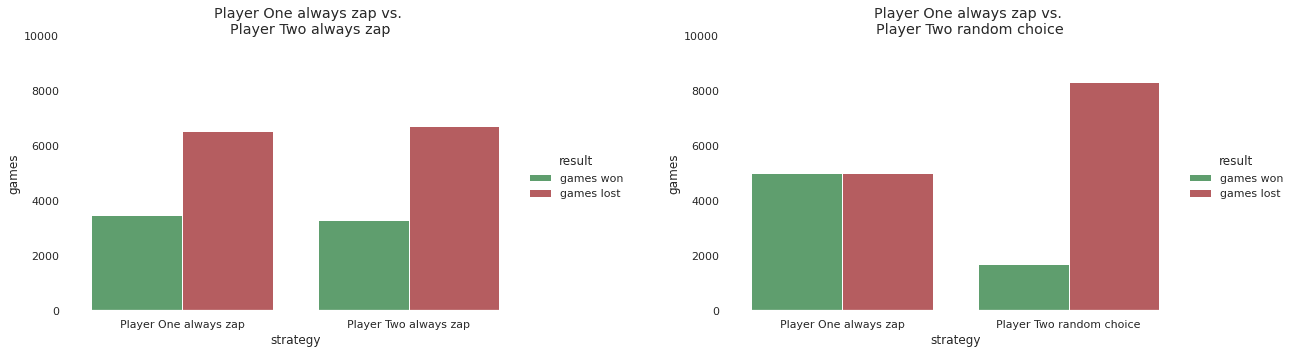
On the surface, it seems like we could conclude that Always Zap is the best strategy to use here, but that does not account for the fact that this strategy is relatively easy to detect and punish in this game. Since robots cannot shoot, If you are playing the always zap strategy, then whenever you offer to shake, you must be a robot!

A way you can combat this is to, when you are human, randomly select between zapping and shaking, biasing towards zapping. To make sure this strategy was viable, I generated strategies that would bias toward shaking and zapping for all integer values between 1 and 99:

def format_text(zap, shake):
  return """
def strategy_random_choice_{zap}_to_{shake}(player, hist):
  if not player.is_human: return Choices.Shake:
  return choices(
    population=[Choices.Zap, Choices.Shake],
    weights=[0.{zap},0.{shake}],
    k=1    )""".format(zap=zap, shake=shake)

if __name__ == "__main__":
  for zap in range(1,100):
    shake = 100 - zap
    text = format_text(zap, shake)
    print(text)

I took these and the original strategies, played them against each other again, and then ranked them by which strategy had the most wins. Then I reduced the sample size to bias toward zapping in degrees of 10 since the results indicated that the precision level was unnecessary.

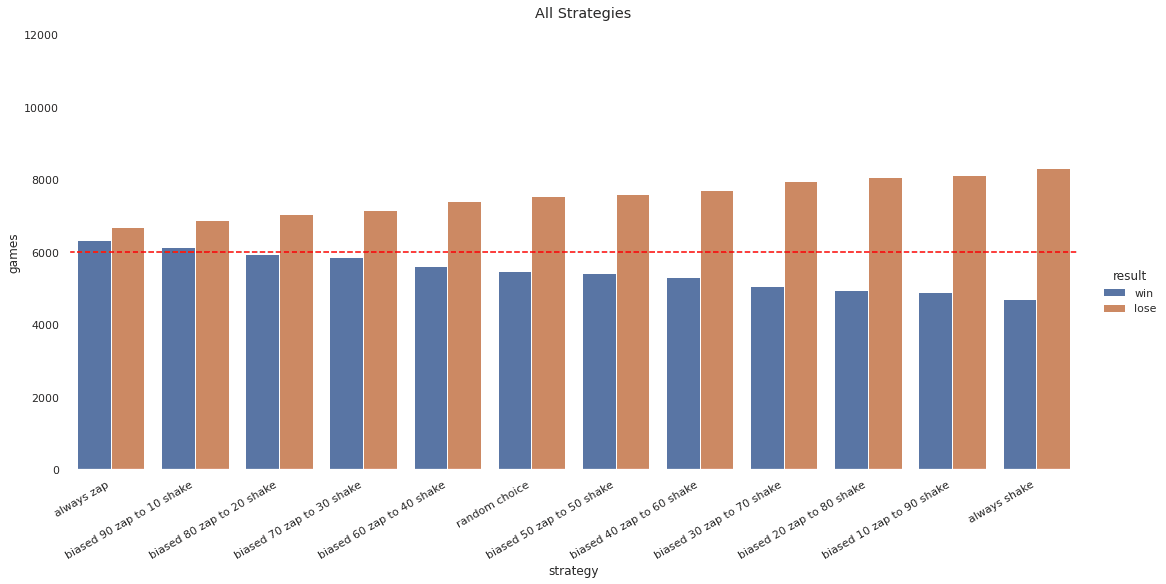
Observations:

• strategies that bias toward zapping perform better than random chance
• always zap is still better than anything else if strategies are naive

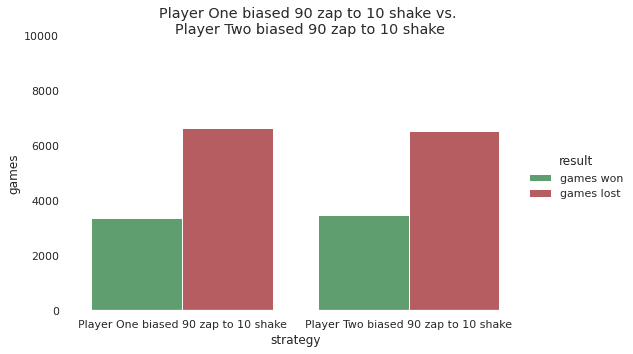
To find out which one of the biased strategies to pick, I then played them all against each other and collected the same win statistics. Zapping 90% of the time also performs the best out of strategies biased towards zapping when played against each other.

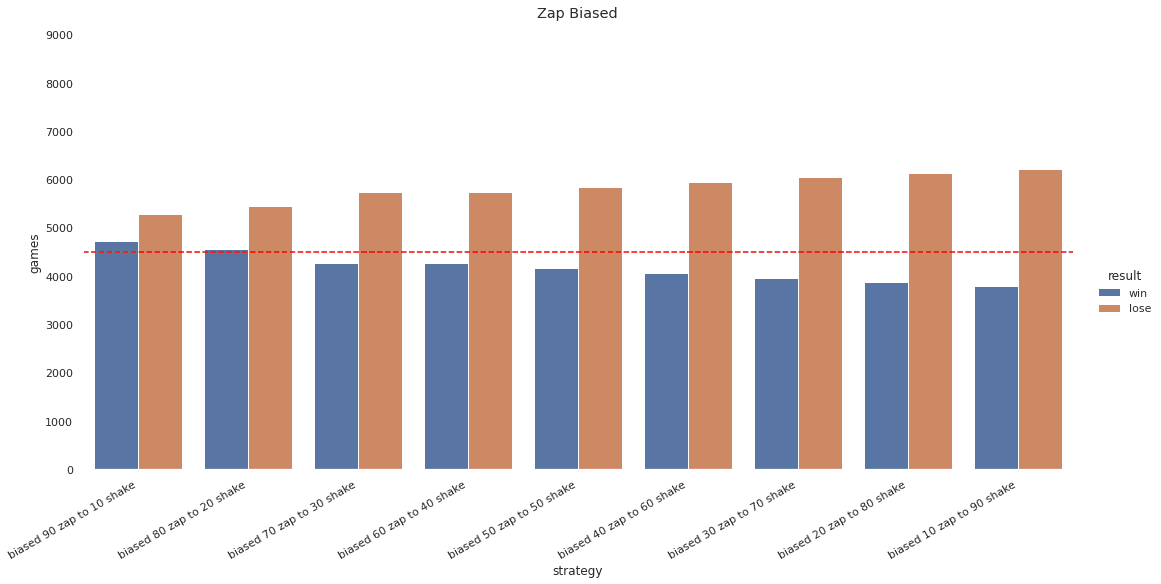
When playing 90% Biased against itself, it also reaches an equilibrium.****

Conclusion

We observed that for this game, three basic strategies could be applied. When these strategies were played against each other, it became clear that this game was a prisoner's dilemma, but there was a twist in the standard strategy since robots cannot shoot. To combat the predictability of always zap, we can modify our strategy for defection to be less predictable by introducing randomness.

Now that we have a strategy for defection, the standard rules of a prisoner's dilemma apply. If you plan on playing this game with someone once and only once, you should always zap. If you plan on playing this game for a few rounds with your opponent, you should try to convince them to always shake. If they start zapping, you should zap them 90% of the time when you are human until they agree to start playing always shake again (aka tit for tat).

Additional Considerations

The rules don't outline who moves first or second, so there could theoretically be a stalemate. However, I didn't model this since I thought it was a little boring since it would probably lead to many stalemate strategies, which don't work well in social settings. The recommended strategy of zap 90% of the time is probably not optimal, but it works well enough for me in practice, and I don't know how to calculate the optimal weights here.

It's hard for humans to be random! I carry dice with me to help me add randomness to situations, but sometimes people will ban the use of dice in games, so you have to get creative. For this one, If I can find a clock on the wall that has seconds, whenever I'm human and the second's value ends with 3, I will shake. It's not perfect, but it's close!

Here's a link to the git repo to try this yourself https://github.com/brevdev/AreYouARobot, and if you'd like to try it using my Jupyter notebook environment, create a Brev environment with this git repo here: https://console.brev.dev.